1970’li yıllara kadar kriptoloji simetrik anahtarlara dayalıydı. Yani şifre çözülürken de aynı anahtarın kullanılması gerekiyordu. Gönderici ve alıcı aynı ortamda bulunmadığı için aynı anahtarı üretmek imkânsızdı. Diffie-Hellman anahtar değişimi gibi yöntemler kullanılarak anahtarlar değiş tokuş edilebilse bile burada da başka sorunlar ortaya çıkıyordu. Örneğin; bir kişi mesajını binlerce kişiye göndermeye çalıştığında herkes ile anahtar paylaşımı yapması gerekiyordu. Peki bunun daha efektif bir yolu var mıdır?
Açık anahtarlı şifreleme
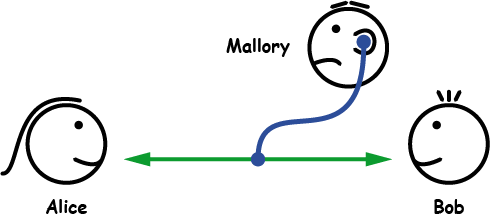
Aslında çok basit bir mantığa dayanmaktadır. Alice bir anahtar alır ve anahtarını saklar. Anahtarı açık bir şekilde Bob’a gönderir. Bob mesajını kilitler ve tekrar Alice’e gönderir. Alice sakladığı anahtar ile kilidi açar ve mesajı okur. Bunu renkler üzerinde daha basitleştirerek anlatan resmi inceleyebilirsiniz.
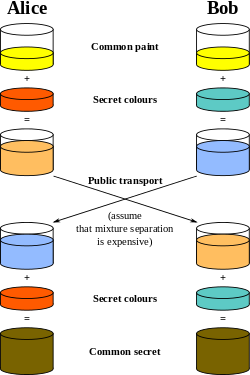
Yukarıda anlattığımız yöntemin matematiksel bir karşılığı olması gerekir. Bunu da 1973 yılında Clifford Cocks buldu. Cocks’un bulduğu bu fonksiyon ileri yönlü çok hızlı çalışmakta ama fonksiyonu geri çevirirken çok çok yavaş çalışmaktadır. Daha da somutlaştırmak gerekirse;
Alice’in göndereceği mesajı m sayısına çevirdik. Alice m sayısının e üssünü aldı ve mod N işlemi yaptı.
me mod N=c c sayısını bulmak çok kolaydır. Ama ?e modN=c ? ulaşmak çok çok zordur.
me mod N=c bu bizim matematiksel kilidimiz. Şimdi de anahtarımız elde edelim;
c sayısının d üssünü alıyoruz.
cd mod N=m yani; med mod N=m olur. Bu işlemimizde e şifreleyici d ise şifre çözücüdür. e ve d sayılarını oluşturmak için ise öklidden yararlanacağız. Öklid bir sayının bir tane asal çarpan kümesine sahip olacağını göstermiştir.
Yazdığımız bir program vasıtasıyla aşağıdaki işlemi kolayca yapabiliriz.
46465161*416161=?
46465161 sayısını asal çarpanlara ayırmak çok daha zordur. Yani yazdığımız programın zaman karmaşıklığı exponansiyel olarak artar. Burada dikkatiniz çekmem gereken konu bu algoritmanın kırılması imkansız değildir ama time complexity(alan karmaşıklığı) çok çok fazladır. 100 basamaklı iki tane asal sayı seçelim. Bu iki sayıyı çarptığımızda basamak sayısı 300’den fazla yeni bir sayı elde ederiz.
p*q=N bu işlem çok kısa sürer. N sayısının asal çarpanlarını yani p ve q yi saklıyoruz. N sayısını istediğimiz gibi dağıtabiliriz. Çünkü N sayısının asal çarpanlarını bulmak yıllar alacak bir işlemdir.
φ(n) = (p-1)(q-1) n sayısının çarpanlarını biliyorsak φ(n) sayısını da kolayca elde edebiliriz. Peki φ(n) fonksiyonunu modüler olarak üs almayla nasıl ilişkilendirebiliriz? Burada Euler teorisine başvurmamız gerekiyor. Konumuzu daha da dağıtmamak için burayı karıştırmıyorum.
Alice Bob’a mesaj göndermek istediğinde şu işlemleri uygulaması gerekir;
- Alice p ve q olmak üzere iki tane çok büyük asal sayı seçer
- N=p*q ile N sayısı hesaplar.
- φ(n) = (p-1)(q-1) fonksiyonu ile N sayısının totient değerini hesaplar.
- 1 < e < φ(N) ve EBOB(e, φ(N)) = 1 şartını sağlayacak “e” sayısı seçer bu sayı küçük olursa mod ve üs alma işlemlerinde daha performanslı çalışabiliriz.
- e ≡ 1 (mod φ(N)) d sayısı hesaplar. Bu değer genişletilmiş Öklid algoritması ile hesaplanabilir.
- me mod N=c şifrelenmiş metin gönderir.
Bob şifreyi çözmek isterse m=cd mod N fonksiyonu ile şifreyi çözer ve mesajı okur.
Örnek;
- p=53 q=59
- N=53*59=3127
- φ(n)=(53-1)*(59-1)=3016
- e=3
- d=(2*(3016)+1)/3=2011
- 893 mod 3127=1394
- 13972011=89 mod 3127
Yararlandığım kaynaklar
http://www.di-mgt.com.au/rsa_alg.html#note6
https://en.wikipedia.org/wiki/Diffie%E2%80%93Hellman_key_exchange
https://tr.wikipedia.org/wiki/RSA#Euler_teoremi_ile_ispat.C4.B1
Bir yanıt yazın